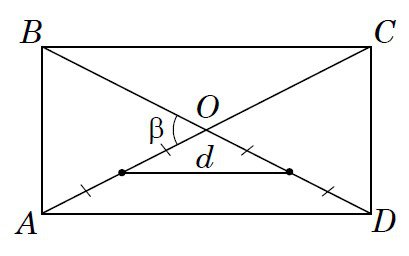
Діагоналі BD і AC прямокутника ABCD перетинаються в точці O, ∠AOB = β (див. рисунок). Відстань між серединами відрізків AO і DO дорівнює d. Знайдіть площу цього прямокутника.
| А | \(2d^2 tg\frac{\beta}{2}\) |
|---|---|
| Б | \(4d^2 tg\frac{\beta}{2}\) |
| В | \(4d^2 sin\frac{\beta}{2}\) |
| Г | \(\frac{4d^2}{tg\frac{\beta}{2}}\) |
| Д | \(\frac{2d^2}{cos\frac{\beta}{2}}\) |
Правильна відповідь
А
Б
В
Г
Д
