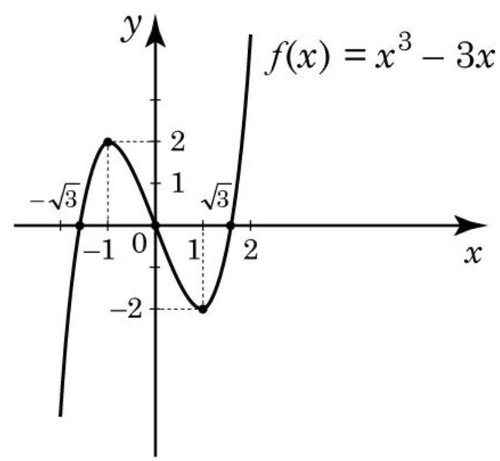
Задано функцію \(y=x^3-3x\)
1. Для наведених у таблиці значень аргумента \(x\) визначте відповідні їм значення \(y\) .
| x | y |
|---|---|
| 0 | |
| -1 | |
| 2 |
2. Визначте й запишіть координати точок перетину графіка функції \(y=x^3-3x\) із віссю x.
3. Знайдіть похідну \(f'\) функції \(f(x)=x^3-3x\).
4. Визначте нулі функції \(f'\).
5. Визначте проміжки зростання i спадання, точки екстремуму й екстремуми функції \(f\).
6. Побудуйте ескіз графіка функції \(f\)
Правильна відповідь
1.
| x | y |
|---|---|
| 0 | 0 |
| -1 | 2 |
| 2 | 2 |
2.
\((-\sqrt(3);0); (0;0); (\sqrt(3);0)\)
3.
\(f'(x)=3x^2-3\)
4.
\(x=1 ; x =-1.\)
5.
Проміжки зростання: \((-\infty; -1], [1; +\infty);\)
проміжок спадання: \([-1: 1];\)
точки екстремуму: \(x_{max}=-1; x_{min}=1;\)
екструмуми: \(f_{max}=2; f_{min}=-2;\)
6.
